[leetcode] Minimum Cost to Make at Least One Valid Path in a Grid

Minimum Cost to Make at Least One Valid Path in a Grid

Algorithm: bfs Created: Mar 04, 2020 4:35 PM DoubleChk: No Type: LeetCode level: 3 link: https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/

Given a mxn grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell.

The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some invalid signs on the cells of the grid which points outside the grid.

You will initially start at the upper left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path doesn’t have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

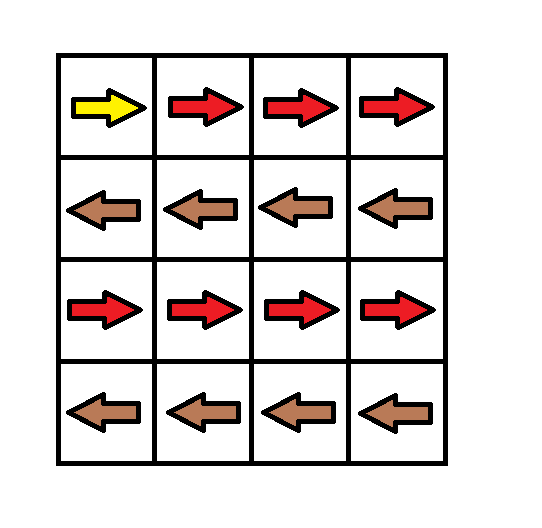
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

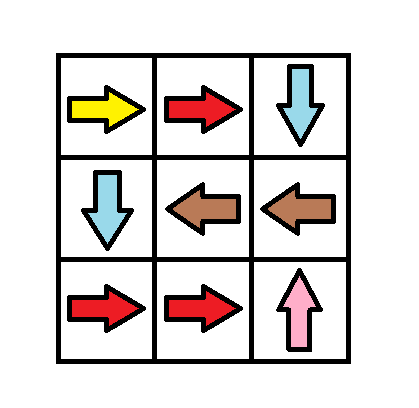
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

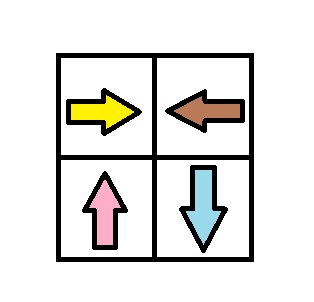
Input: grid = [[1,2],[4,3]]
Output: 1

Example 4:

Input: grid = [[2,2,2],[2,2,2]]
Output: 3

Example 5:

Input: grid = [[4]]
Output: 0

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100

---

    class Solution {
    public:
        int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, { -1, 0}};
        queue <pair<int, int>> q;
    
        int minCost(vector<vector<int>>& grid) {
            
            int cost = 0;
            int m = grid.size();
            int n = grid[0].size();
            vector<vector<int>> dp(m, vector<int>(n, INT_MAX));
            
            dfs(grid, 0, 0, cost, m, n, dp);
            
            while(!q.empty()){
                cost++;
                int sz = q.size();
                
                for(int i=0; i<sz; i++){
                    pair<int, int> p = q.front();
                    int px = p.first;
                    int py = p.second;
                    q.pop();
                    
                    for(int j=0; j<4; j++){                
                        dfs(grid, px + dir[j][0], py + dir[j][1], cost, m, n, dp);
                    }
                }
                
            }
            
            return dp[m-1][n-1];
        }
        
        void dfs(vector<vector<int>>& grid, int x, int y, int cost, int m, int n, vector<vector<int>>& dp){
            if(x >= m || y >= n || x < 0 || y < 0 ||dp[x][y] != INT_MAX) return;
            dp[x][y] = cost;
            q.push(make_pair(x, y));
            
            int next_dir = grid[x][y] - 1;
            dfs(grid, x + dir[next_dir][0], y + dir[next_dir][1], cost, m, n, dp);
        }
    };
    

• 문제풀이

  1. dfs로 방문 가능 한 모든 곳 탐색

  2. 방문한 노드들을 queue에 삽입, visit 체크

  3. 큐를 돌면서 상하좌우 탐색

• 후기

  3레벨 첨풀어봐 ㅎㅅㅎ